2019学年长宁区协和学校初一（上）数学第二次月考考试试题
（考试时间90分钟，满分100分） 2019.12
填空题（本大题共15题，每小题2分，满分30分）
用代数式表示“x与y的相反数的和”__________.
单项式
的系数是__________.
计算：
__________
若
与
是相同种类项，则
__________.
若分式
有意义，则x的取值范围是__________.
把
写成只含有正整数指数幂的形式，其结果为__________.
数据0.00000032用科学计数法可表示为__________.
若4a+3b=1，则8a+6b-3=__________.
化简：
__________.
计算：
__________.
假如
，那样m =__________.
正三角形ABC是轴对称图形，那样它的对称轴共有__________条.
如图1，，△ABC的周长为12，把△ABC的边AC对折，是点C与点A重合，折痕交BC边于点D，交AC边于点E，联结AD，若AE=2，则△ABD的周长__________.
甲乙两家商店9月份销售额均为a元，在11月份和12月份两个月中，甲商店的销售额平均每月增长x%，乙商店的销售额平均每月降低x%，11月份甲商店的销售额比乙商店的销售额多__________万元.
已知图2，大正方形的边长为4厘米，小正方形的边长为2厘米，起始状况如图2所示，大正方形固定不动，把小正方形向右平移，当两个正方形重叠部分面积为2平方厘米始，小正方形平移的距离为__________厘米.
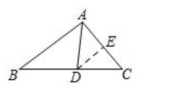
图1 图2
选择题（本大题共5题，每题2分，满分10分）
下列计算正确的是···········································（ ）
A． B. 
C. D.
下列多项式能因式分解的是···································（ ）A.
B. 
C. 
D. 
假如一个正多边形绕着它的中心旋转6零零后，能与原正多边形重合，那样这个正多边形是····················（ ）
A．是轴对称图形但不是中心对称图形 B.既是轴对称又是中心对称图形
是中心对称图形但不是轴对称图形 D.不是轴对称又不是中心对称
计算
·的结果为··························（ ）
A. 
B. 
C. 
D.
若则下列判断结果正确的是·······················································（ ）
A. 
B. 
C. D. 
简答卷（本大题共6题，每小题5分，满分30分）
计算：
22.计算：
23.计算： 24.分解因式：
24.分解因式：
26.解方程：
简答卷（本大题共4题，第27、28每题6分，第29题8分，第30题10分，满分30分）
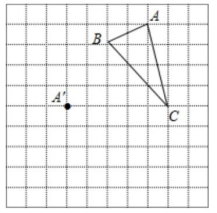
27.在正方形网格中，每一个小正方形的边长均为1个长度单位，△ABC三个顶点的地方如图所示，现将△ABC平移，使点A移动到A’，点B’、点C’分别是B、C的对应点；
（1）请画出平移后的B’点；
（2）点A’绕点B’按逆时针方向旋转9零零后，它经过的路线是什么样的图形？画出这个图形。
28. 先化简，再求值：
，其中
.
29.小丽、小明训练打字，已知小丽比小明每分钟多打80个字，小丽打3500个字的时间与小明打2500个字的时间相同。
（1）小丽、小明每分钟分别可打多少字？
（2）假如有一份总字数为m的稿件需要输入电脑，小丽工作了a个小时后剩余的输入工作由小明继续完成，则小明还需要工作多少小时？（所得结果用含有m、a的代数式表示；m、a均为大于零的正数）
30.如图，将直接三角形ABC绕着直角顶点C逆时针旋转900，得到△A1B1C，将△A1B1C向右平移，使点B1与点A重合，得到△A2AC2，设BC=a，AC=b
（1）试画出△A1B1C和△A2AC2
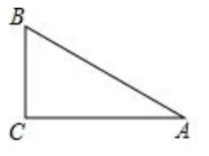
（2）联结A2B，用a，b表示△AA2B的面积；
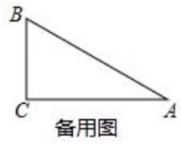
（3）若上述平移的距离为6，△AA2B的面积为8，试求△ABC的面积；
